Extension

Warning

This material is not required by the GCSE.

It can sometimes be hard to see the point of logic gates at this level. It is true, though, that ALL operations carried out by the computer must be done by using logic gate circuits. Even something as simple as adding two numbers together!

x = 3 + 2

Such an addition looks simple enough, but under the hood this operation has to be carried out using logic gates and associated Boolean operations - known as bit-wise operations.

This section looks at how this is done.

Binary addition

We'll start with two numbers we want to add, A and B in binary:

A (3) = 0011
B (2) = 0010

Bit-wise operations

We'll use the following Boolean operations:

AND (logical AND, denoted by &)
XOR (exclusive OR, denoted by ^)
NOT (logical NOT, denoted by ~)

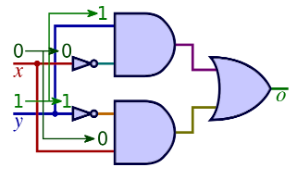
Half Adder

A half adder is a simple circuit that adds two single-bit numbers. When we add two binary digits together we get the following:

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 Carry 1

So we need two outputs, a sum and a carry.

We can implement a half adder using Boolean operations as follows:

S (sum) = A XOR B
C (carry) = A AND B

As a truth table this is:

A	B	S (Sum)	C (Carry)
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

In this table:

A and B are the input bits
S (Sum) is the output sum bit
C (Carry) is the output carry bit

The truth table shows that:

When both A and B are 0, the sum is 0 and there's no carry
When A is 0 and B is 1, the sum is 1 and there's no carry
When A is 1 and B is 0, the sum is 1 and there's no carry
When both A and B are 1, the sum is 0 and there's a carry of 1

Full Adder

To add together more than one binary digit we need to combine two half adders and a third input for the carry from the previous bit position.

The step by step process is:

Add the least significant bits (LSBs) of A and B using a half adder:
- S0 = A0 XOR B0
- C0 = A0 AND B0
Add the next bit positions of A and B using another half adder, considering the carry from the previous step:
- S1 = A1 XOR B1 XOR C0
- C1 = (A1 AND B1) OR (A1 AND C0) OR (B1 AND C0)
Repeat step 2 for each subsequent bit position until we reach the most significant bits (MSBs).

Example: Adding 3 and 2 using Boolean Operations

Let's add 3 and 2 using the full adder implementation:

A (3) = 0011 (binary)
B (2) = 0010 (binary)

Add LSBs:

S0 = A0 XOR B0 = 1 XOR 0 = 1
C0 = A0 AND B0 = 1 AND 0 = 0

Add next bit positions:

S1 = A1 XOR B1 XOR C0 = 0 XOR 1 XOR 0 = 1
C1 = (A1 AND B1) OR (A1 AND C0) OR (B1 AND C0) = (0 AND 1) OR (0 AND 0) OR (1 AND 0) = 0
Add next bit positions:
S2 = A2 XOR B2 XOR C1 = 0 XOR 0 XOR 0 = 0
C2 = (A2 AND B2) OR (A2 AND C1) OR (B2 AND C1) = (0 AND 0) OR (0 AND 0) OR (0 AND 0) = 0
The result is S2 S1 S0 = 0101, which represents the sum 5 in binary.

While this process may seem cumbersome, it demonstrates how Boolean operations can be used to perform arithmetic operations like addition. In reality, digital circuits use more efficient implementations, such as carry-lookahead adders or parallel adders, to perform arithmetic operations.

Implementation using Python

Implementing binary addition using Boolean operations in Python can be an interesting exercise. Here's a possible implementation:

def binary_add(A, B):
    # Convert integers to binary strings
    A_bin = bin(A)[2:]  # Remove '0b' prefix
    B_bin = bin(B)[2:]  # Remove '0b' prefix

    # Ensure both binary strings have the same length
    max_len = max(len(A_bin), len(B_bin))
    A_bin = A_bin.zfill(max_len)
    B_bin = B_bin.zfill(max_len)

    # Initialize result and carry
    result = ''
    carry = 0

    # Iterate through each bit position
    for i in range(max_len - 1, -1, -1):
        # Extract current bits
        A_bit = int(A_bin[i])
        B_bit = int(B_bin[i])

        # Calculate sum and carry using Boolean operations
        sum_bit = (A_bit ^ B_bit) ^ carry
        carry = (A_bit & B_bit) | (A_bit & carry) | (B_bit & carry)

        # Append sum bit to result
        result = str(sum_bit) + result

    # If there's a remaining carry, add it to the result
    if carry:
        result = str(carry) + result

    # Convert binary result back to an integer
    return int(result, 2)

# Example usage:
A = 3
B = 2
result = binary_add(A, B)
print(f"The sum of {A} and {B} is {result}")  # Output: 5

This implementation uses the same principles as the step-by-step process described earlier.

It converts the input integers to binary strings, iterates through each bit position, and uses Boolean operations to calculate the sum and carry. Finally, it converts the binary result back to an integer.

Keep in mind that this implementation is not optimized for performance and is intended for educational purposes only. In practice, you would use Python's built-in arithmetic operators for addition, which are much faster and more efficient.