Skip to content

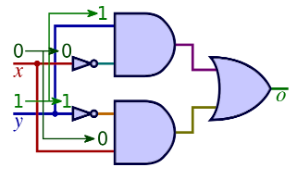
Introduction to Logic Gates

In computer science and mathematics, logic is a way of making decisions based on certain conditions being either true or false. In digital circuits, logic helps us control how electronic devices work by making decisions based on whether inputs (conditions) are on or off, which can also be thought of as true or false.

In simple terms:

  • True is represented as 1
  • False is represented as 0

You will already use logic in everyday life, without even realizing it.

For example:

"If it's sunny AND I have time, I'll go for a walk."

In this case, going for a walk depends on two things being true: the weather is sunny, and you have time.

Similarly, computers and digital circuits make decisions based on inputs that are either true (1) or false (0). These decisions are controlled by logic gates, which perform logical operations.

Inputs and Outputs: True or False

A logic gate takes inputs (true or false values, 0 or 1) and produces an output that depends on the type of gate. Each gate follows a set of rules about how to combine its inputs to determine the output.

For example, let’s consider two conditions:

  • A: "It is raining."
  • B: "I have an umbrella."

We can use logic gates to make decisions based on these inputs.

Key Logic Gates: AND, OR, NOT and XOR

We have three ways of representing these logic gates and the circuits that can be designed using these gates:

  • Truth table
  • Boolean expression
  • Logic Diagram

Each depicts the same process and well consider each n the following sections.

AND Gate

The AND gate checks if all the inputs are true. It outputs true (1) if, and only if, both inputs are true. Otherwise, it outputs false (0).

Imagine the following scenario:

You will go to the cinema if:

  • A: You have enough money for a ticket
  • B: There's something you want to see at the cinema

You need both the money for the ticket, and something that interests you at the cinema. If either is missing then you will not go.

We have already encountered something similar when programming:

1
2
3
4
if (A == 1 and B == 1) then
    print("You can go the cinema")
else
    print("You can  not go to the cinema")

We can represent all of the possible conditions for this statement by using truth table:

Truth Table for AND:

A (Money) B (Interesting Movie) A AND B (Go to the cinema)
0 0 0
0 1 0
1 0 0
1 1 1

The AND gate only outputs 1 (True) when both inputs A and B are 1 (True). When either of these conditions is False you will not be going to the cinema.

Boolean expression for AND

This scenario can also be represented using a boolean expression: \(A \bullet B\)

Note

A boolean expression is an expression using special algebraic notation. Inputs are denoted by capital letters e.g. A, B etc. The operators used are:

  • AND: \(A \bullet B\)
  • OR: \(A + B\)
  • NOT: \(\overline A\)

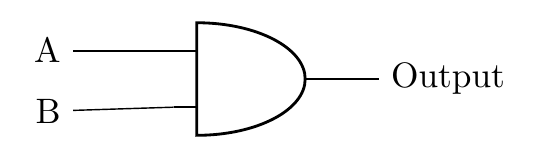
Logic diagram

The symbol for an AND gate:

OR Gate

The OR gate outputs true (1) if at least one of its inputs is true. The only time it outputs false is if both inputs are false.

You may not have the money for a ticket, but perhaps a friend is willing to pay for you? (We'll ignore what might be on at the cinema!)

Now we have the following inputs:

  • A: You have money for a ticket
  • B: Your friend is will to pay for your ticket
1
2
3
4
if (A == 1 or B == 1) then
    print("You can go to the cinema")
else
    print("You can not go to the cinema")

Again, we can describe these conditions using a truth table:

Truth Table for OR:

A (Money) B (Friend pays) A OR B (Go to the cinema)
0 0 0
0 1 1
1 0 1
1 1 1

Logic Diagram

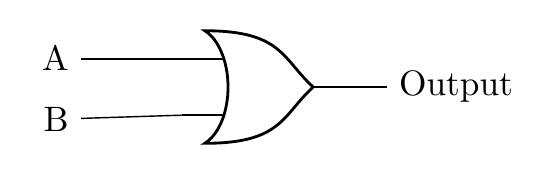
Explanation:

The OR gate outputs 1 (True) if either input A or input B (or both) is 1 (True). This means you’ll go to the cinema if you have the money (A = 1), if your friend will pay for your ticket (B = 1), or both.

In these OR gate scenarios, the outcome is true (you go to the cinema) if either one of the conditions is met. This contrasts with the AND gate logic, where both conditions must be true. With OR, just having one true input is enough for the output to be true.

This scenario can also be represented using a boolean expression: \(A + B\)

NOT Gate

The NOT gate does something simple: it inverts the input. If the input is true (1), the output will be false (0), and if the input is false (0), the output will be true (1).

The NOT gate takes only one input, either True (1) or False (0).

Our cinema analogy might might break down a little, but we can consider the scenario that says we will go to the cinema when the sun is not out!

We have the following conditions:

  • A: It is sunny (the input)
  • NOT A: It is not sunny (the output, and we go to the cinema)

In this case, you are more likely to go to the cinema if it's not sunny (i.e., a rainy or cloudy day). So the condition A checks whether it’s sunny, and the NOT gate inverts that. If it’s sunny (A = 1), you won’t go to the cinema (output = 0). If it’s not sunny (A = 0), the NOT gate outputs true, meaning you’ll go to the cinema.

1
2
3
4
if not(A) then
    print("You can go to the cinema")
else
    print("You can not go to the cinema")

Truth Table for NOT:

A (Sunny) NOT A (Not sunny, go to the cinema)
0 1
1 0

Logic Diagram

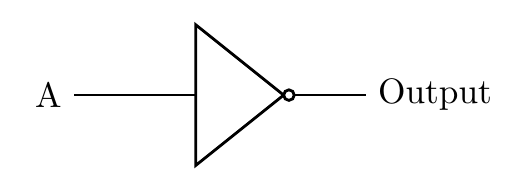
Explanation of the NOT Logic:

  • If A (it’s sunny) is false (0), then the NOT gate outputs true (1), meaning you’ll go to the cinema.
  • If A (it’s sunny) is true (1), the NOT gate outputs false (0), meaning you won’t go to the cinema because it's sunny and you're more likely to do something outdoors.

This scenario can also be represented using a boolean expression: \(\overline A\)

XOR Gate

The XOR gate (exclusive OR) behaves differently from the OR gate because it only outputs true (1) when exactly one of the inputs is true—not both. In a real-life scenario, this would mean you make a decision when one condition is met, but not if both conditions are true or both are false.

Scenario: Cinema or Streaming at Home

You will either:

  • Go to the cinema or
  • Stream a movie at home, but not both at the same time.

Conditions

  • A: You have enough money to go to the cinema.
  • B: A good movie is available to stream at home.

Thus:

  • You’ll go to the cinema if you have the money but not a good movie to stream.
  • You’ll stream at home if a good movie is available but you don’t have the money to go out.
  • If both conditions are true (you have money and a good movie to stream), you can’t do both at the same time, so you’ll choose neither.
  • If neither is true, you can’t go to the cinema or stream, so you’ll do something else.

Boolean expression

\(A \text{ XOR } B\)

or

\(A \oplus B\)

Truth Table for Cinema vs. Streaming XOR Decision:

A (Have Money for Cinema) B (Good Movie to Stream) Output (Cinema or Stream)
0 0 0
0 1 1
1 0 1
1 1 0

Logic Diagram

The symbol used for the XOR gate:

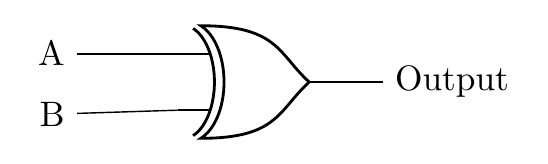
Explanation of the XOR Logic:

  • When both A and B are false (0, 0): You don’t have money for the cinema, and there’s no good movie to stream, so you won’t do either (output = 0).
  • When A is false and B is true (0, 1): You don’t have money to go to the cinema, but there’s a good movie to stream at home, so you stream (output = 1).
  • When A is true and B is false (1, 0): You have money to go to the cinema, but there’s nothing good to stream, so you go to the cinema (output = 1).
  • When both A and B are true (1, 1): You have money to go to the cinema, and there’s a good movie to stream, but you can’t do both, so you do neither (output = 0).

The XOR gate works well here because it captures the decision-making process where you only do one of the two activities, not both. If one condition is true, you take action (go to the cinema or stream). If both conditions are true, you can’t choose both, so you end up doing neither.