Combining Logic Gates
Having looked at the basic gates (AND, OR, NOT and XOR) we now move to looking how these can be combined to make more complex decisions.
Scenario: Going to the Cinema

You will go to the cinema if:
- A: You have money for a ticket.
- B: A friend is available who can pay for your ticket.
- C: It is not sunny.
We have three inputs for our decision.
You will go to the cinema if:
- You have money (A) OR your friend is willing to pay (B).
- It is not sunny (NOT C) (because you prefer to go indoors when it's not sunny).
So, the logic combines:
- A OR B: You need either money or a friend who will pay for the ticket.
- NOT C: You will only go if it's not sunny.
The full boolean expression becomes:
\((A \text{ OR } B) \text{ AND } \text{NOT } C\)
Or in formal notation:
\(( A + B) \bullet \overline C\)
Logic Diagram
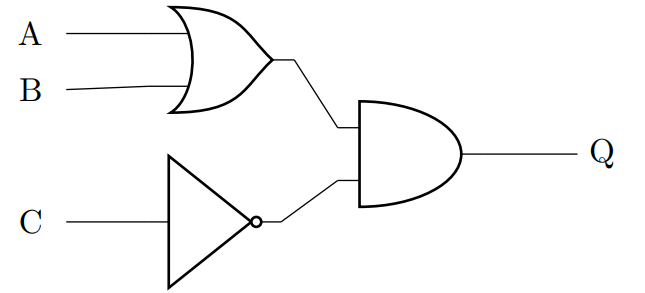
Explanation of the Logic
- A OR B: You either have money (A) or a friend to pay (B) for your ticket.
- NOT C: It needs to be not sunny (C) to prefer going to the cinema.
- The combination: You’ll go to the cinema if either you or your friend has money and it’s not sunny.
Truth Table for the Full Scenario:
| A (Money) | B (Friend) | C (Sunny) | NOT C (Not Sunny) | Output (Go to Cinema) |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
Explanation:
You will go to the cinema if:
- You have money (A = 1) or your friend can pay (B = 1).
- It is not sunny (NOT C = 1).
The only time you won’t go is if you:
- Have no money (A = 0) and no friend to pay (B = 0).
- It is sunny (C = 1).