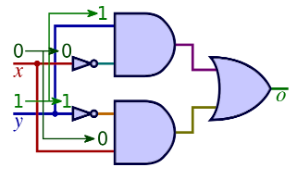
Example
Here, we'll take a scenario and create the:
- truth table
- boolean expression, and
- logic diagram
It is a popular examination question and you will be required to any, or all, of these from a given scenario.
Scenario

A coffee machine can be turned on if:
- The coffee beans container is not empty AND the water reservoir is not empty OR the machine is in "cleaning mode"
Analyse the scenario carefully. Look for the keywords of AND and OR , also where there may be a negative meaning indicating a NOT.
To model the logic of this system we need an AND gate, also an OR gate:
- AND gate: Coffee beans container is not empty AND Water reservoir is not empty
- OR gate: ((Coffee beans container is not empty AND Water reservoir is not empty) OR Machine is in cleaning mode)
There is also a NOT gate here too:
- NOT gate: Coffee beans container is NOT empty
Creating the Truth Table
To build the truth table, we have three inputs and we need to note all the possible permutations of when these inputs are either true or false.
Our inputs are:
- Coffee beans
- Water reservoir, and
- Machine in cleaning mode
You can use A, B or C for each of these if you wish. They are just labels of course.
Note
With 3 inputs there will be 8 possible permutations because \(2^3 = 8\)
When writing the permutations keep to the sequence that moves from where each is 0, or False through to each one being 1, or True.
| Coffee Beans (A) | Water Reservoir (B) | Machine in Cleaning Mode (C) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
The complete the output column by evaluating the expression carefully. The first row is easy, when any of our inputs are false then the coffee machine will not work:
| Coffee Beans | Water Reservoir | Machine in Cleaning Mode | Coffee Machine |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
The second row puts in the coffee machine in cleaning mode, and so it can be turned on. it does not matter about either the coffee beans container nor the water reservoir:
| Coffee Beans | Water Reservoir | Machine in Cleaning Mode | Coffee Machine |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
The third row says there is water in the reservoir but no coffee beans have not been added, and the machine if not in cleaning mode. Therefore, the coffee machine will not work as we have to have both coffee beans and water.
| Coffee Beans | Water Reservoir | Machine in Cleaning Mode | Coffee Machine |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
Continue through with each row until you arrive at the following truth table for all the possible permutations:
| Coffee Beans | Water Reservoir | Machine in Cleaning Mode | Coffee Machine |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Creating the Boolean Expression
The Boolean expression for this circuit is:
Coffee Machine = (Coffee Beans AND Water Reservoir) OR Machine in Cleaning Mode
or
\(Q = (A \bullet B) + C\)
This expression evaluates to TRUE if the coffee machine can be turned on, and FALSE otherwise.
Creating the Logic Diagram
Creating the logic diagram can be a challenging task, but with a clear approach, you can master it.
You can either:
- Start with the output and work backwards, or
- start with the inputs and move forward
Start with the output and work backwards
This approach is often recommended because it helps you focus on the desired outcome and then break it down into smaller, manageable components.
- Identify the output: The output is "Machine can be turned on". Conventionally, we label this as Q
-
Determine the conditions: For the machine to be turned on, one of the following conditions must be true:
- The coffee beans container is not empty (A) AND the water reservoir is not empty (B)
- OR the machine is in "cleaning mode" (C)
-
Connect the conditions to the output The final condition is the OR gate, so draw that symbol and connect its output to Q
- Connect the inputs to most recently added gate: The inputs to the OR gate will be:
- the output from an AND gate
- C, the cleaning mode
- Label the inputs We will have added an AND gate in the previous step, so all that remains is to label the inputs to that gate with A and B
Start with the input and move forwards
This approach can also be effective, especially if you're more comfortable thinking about the inputs and how they interact with each other. Here's how:
- Identify the inputs
- A Coffee beans container
- B Water reservoir
- C Cleaning mode
-
Determine the relationships
- A and B are connected by an AND gate, so add this to the diagram
- the output of the AND gate is connected to one of the inputs to the OR gate
- C is connected to the other input of the OR gate
- The output of the OR gate is connected to Q
Once you've created the logic diagram, test it with different input combinations to ensure it produces the correct output.
This can be challenging but the more you practice creating logic diagrams, the more comfortable you'll become with the process.