Searching Algorithms

Objectives

• Understand the concept of linear search as a sequential algorithm for finding a specific element in a list.
• Know how to implement a linear search algorithm in pseudocode and a programming language (e.g., Python).
• Understand the binary search algorithm as a more efficient searching technique that requires a sorted list.
• Know how to implement a binary search algorithm in pseudocode and a programming language (e.g., Python).
• Compare the linear search and binary search algorithms in terms of efficiency and suitability for different scenarios.
• Gain experience in tracing and debugging code for both linear and binary search algorithms.

These learning objectives cover a range of skills and knowledge related to searching algorithms, algorithmic efficiency, coding implementation, and problem-solving in a computer science context.

Sifting through a whole bunch of data looking for a particular item is a very common occurrence, not least when we use a computer. There are a number of algorithms we can use to search for data. Here we look at two:

• Linear Search
• Binary Search

Linear Search

Take something simple as a shopping list e.g.

• Milk
• Eggs
• Tomatoes
• Mince
• Flour

We want to find if a particular item exists in the list, say "Mince". Being human it's trivial to scan through such a short list and find that "Mince" is indeed in the list. We do this so quickly without really thinking about the steps we are taking to arrive at the answer i.e. the algorithm we are using. If we are going to get a machine to do this for us then we need to work through that algorithm.

The item we are looking for is "Mince", this is known as the search key. We have the list of items held as a list of strings, or an array of strings. We compare our search key against the first item in the list: "Milk". "Mince" is not the same as "Milk", so we then move on to the next item in the list. "Eggs", again is not the string we are looking for. We continue to do this until we find "Mince" as the fourth item in the list and we can quit searching.

If we were looking for, say, "Crisps" we would get to the end of the list having not found it as "Crisps" does not exist in our current list.

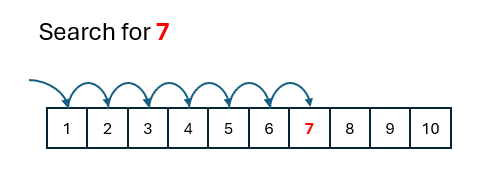
We've carried out a linear search, sometimes called a sequential search. The linear search is a relatively simple searching algorithm that looks for a specific element in a list one by one, checking each element until a match is found or the end of the list is reached.

So, when looking for "Mince" each item is compared to this search key:

Warning

If the animation does not appear, just refresh the page!

Linear Search Animation

Start Search

The process again:

• Start from the beginning of the list.
• Compare the target element with each element in the list sequentially
• If a match is found, return the index of the element; otherwise, continue searching until the end of the list
• If the end of the list is reached without finding a match, indicate that the element is not present.

In Python we can easily write the code for the linear search:

# linear search

shopping_list = ["Milk", "Eggs", "Tomatoes", "Mince", "Flour"]  # initialise the list
item_count = len(shopping_list) 
search_key = "Mince"        # initialise the search key
found = False

for i in range(item_count):
    if shopping_list[i] == search_key:
        found = True

if found:
    print(f"{search_key} is in the list")
else:
    print(f"{search_key} is not in the list")

Notice how we have to start at the beginning of the list and compare the search key with every item in the list. The boolean variable found is set to True if the item is there. In the current algorithm we keep on searching for the item even when it has already been found. This is the worst case behaviour of our algorithm i.e. if n is the length of the list then the worst case means we will be making a total of n comparisons. Our current algorithm is always the worst case! If the item we're looking for is the first item in the list we keep on searching ... what a waste of computing time. We can improve on this by changing the loop in lines 8-10 to:

while i < item_count and found == False:
    if shopping_list[i] == search_key:
        found = True
    i += 1

As soon as we find the search key in our list the loop will terminate. Our best case will not be when the item we're looking for is the first item in the list. The worst case remains, it will be when the search key is the last item in the list (or not in the list).

With such a small number of items this change will make little difference but as the number of items in our list increases, and increases, it will being to have a significant impact on how quickly our algorithm will return a result. Mathematically, computer scientists use something called BigO notation to describe the efficiency of an algorithm. BigO notation is not part of the GCSE syllabus but we would describe the linear search as O(n) where n is the number of items. As n grows so does the time taken for this algorithm to complete (in the worst case).

The study of algorithms is about finding the best algorithm for the given situation.

Note

It would be even better to put this algorithm into its own function passing in the search key and the item list as parameters to this function.

If there is a small dataset, and the items in that dataset are not ordered then a linear search will be fine. However, for large datasets it will very quickly begins to slow down and there is a better alternative, the binary search.

Binary Search

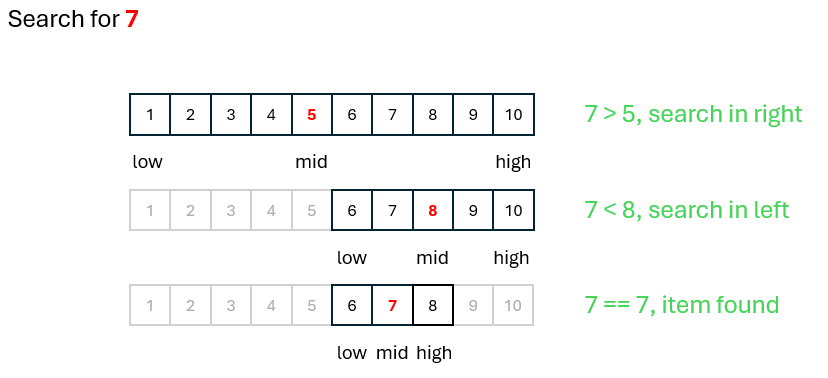
The binary search is a more efficient searching algorithm that requires the list to be sorted. Remember that point, it's a common examination question, the items in the dataset must be sorted.

It works by repeatedly dividing the list of items in half until the target element is found. Think of the children's game of "Guess The Number". It starts with one player thinking of a number between say 1 and 100. We could approach this linearly i.e. "Is it 1?", "Is it 2?", "Is it 3?" etc.. Or we could ask "Is it higher than 50?" If the answer is "yes" then we can automatically discount all the values between 1 and 50 thus chopping the original list in half.

In outline, the binary search works as follows:

• Start with the entire sorted list.
• Compare the target element with the middle element of the list.
• If the target is equal to the middle element, the search is successful.
• If the target is less than the middle element, repeat the search on the lower half of the list.
• If the target is greater than the middle element, repeat the search on the upper half of the list.
• Continue dividing the search interval until the target is found or the interval becomes empty.

A binary search is generally more efficient than linear search for large datasets, especially when the data is sorted. Linear search may require checking every element in the worst case.

It's a more complicated algorithm to implement:

def binary_search(items, target):
    low = 0
    high = len(items) - 1

    while low <= high:
        mid = (low + high) // 2  # Calculate the middle index

        if items[mid] == target:
            return mid  # Element found, return its index
        elif items[mid] < target:
            low = mid + 1  # Discard the left half
        else:
            high = mid - 1  # Discard the right half

    return -1  # Element not found

This implementation defines a function binary_search that takes a sorted list (items) and a target element (target). It returns the index of the target element if found, or \(\(-1\)\) if the element is not in the list.

The function uses a while loop to repeatedly narrow down the search range by adjusting the low and high indices based on the comparison of the middle element with the target.

The function can be called:

sorted_list = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
target_element = 7

result = binary_search(sorted_list, target_element)

if result != -1:
    print(f"Element {target_element} found at index {result}.")
else:
    print(f"Element {target_element} not found in the list.")

Copy the code to the IDE you use for Python programming and try it out. Change the items being searched. They can be strings or floats, the data type does not matter.

Note

In the next section we'll use these algorithms to learn an important skill for debugging programs, that of tracing code.

Warning

If the animation does not appear, just refresh the page!

Binary Search Animation

Start Search

Mathematically, using the Big O notation introduced in the previous section, we can work out the number of "guesses" required or a given number of items:

Number of items in the list (n)	Maximum number of "guesses"
10,000	14
1,000	10
500	9
100	6
50	5
10	3

This is \(O(log_2 n)\)

Questions

1. Why is a linear search also known as a 'sequential search,' and how does it operate on a list?

It compares elements in random order to find the target.

It starts at the end of the list and works backwards.

It checks each element in the list one by one until it finds the target or reaches the end.

It skips every second element to make the search faster.

A linear search works sequentially by comparing each element in the list until the target is found or the entire list is traversed.

Submit

2. Which of the following is a correct pseudocode for a linear search?

FOR each item in list IF item == search_key THEN RETURN index

IF search_key == first_item THEN RETURN 0 ELSE RETURN -1

FOR item in list COMPARE search_key TO item UNTIL FOUND

WHILE search_key NOT FOUND CONTINUE THROUGH LIST

The correct pseudocode iterates through each item in the list and compares it to the search key, returning the index when a match is found.

Submit

3. Convert the following pseudocode into Python code:

FOR each item in list
    IF item == search_key THEN
        RETURN index

for item in list: if item == search_key: return index

for i in range(len(list)): if list[i] == search_key: return i

while list not empty: compare search_key to item and return index

for item in list: if item == search_key: break

The correct Python code uses for i in range(len(list)) to loop through the list and check each item against the search key.

Submit

4. What is the worst-case behavior of a linear search algorithm?

The search key is found at the beginning of the list.

The search key is found in the middle of the list.

The search key is the last item in the list or not present at all.

The search key appears multiple times in the list.

In the worst case, a linear search has to check every item in the list, either finding the target at the end or not finding it at all.

Submit

5. Which of the following describes the main principle of a binary search?

It compares each element in the list one by one.

It sorts the list first before searching.

It divides the list in half, comparing the middle element to the target and repeating the process on the relevant half.

It starts from the last element and works backwards.

Binary search divides the list in half, compares the target with the middle element, and repeats the search on the left or right half depending on the result.

Submit

6. Why does a binary search require the list to be sorted?

Because it compares adjacent elements.

Because it divides the list and compares the middle element, which only works correctly in a sorted list.

Because it must check each item sequentially.

Because sorting makes the search faster.

Binary search works by comparing the middle element and eliminating half of the list at each step, which only works if the list is sorted.

Submit

7. Which of the following pseudocode correctly implements a binary search?

Set low to 0, high to length of list, check middle, adjust low or high and repeat until found.

Start at the first element, move forward by halves, check middle, repeat until found.

Divide list into thirds, check middle element, repeat on one-third until found.

Compare first and last elements, eliminate all but the middle element.

The binary search pseudocode sets initial low and high values, checks the middle element, and narrows the search range by adjusting either low or high.

Submit

8. In Python, which of the following implementations correctly performs a binary search?

while low < high: compare middle element, return if found, else adjust range

while low <= high: calculate mid, compare target with items[mid], adjust low or high accordingly

if target in list: return list.index(target), else return -1

for item in list: if item == target: return item

The correct Python implementation repeatedly calculates the middle index and adjusts the search range based on the comparison with the target.

Submit

9. Which of the following statements correctly compares the efficiency of linear and binary search algorithms?

Linear search is faster than binary search when the list is large.

Binary search is more efficient for large datasets if the list is sorted, while linear search is preferred for smaller or unsorted lists.

Binary search works better for unsorted lists.

Linear search is more efficient than binary search in all cases.

Binary search is more efficient when the list is large and sorted, while linear search is used for unsorted lists or smaller datasets.

Submit

10. Which real-world scenario would be most suitable for a linear search?

Searching for a word in a large dictionary where the words are in alphabetical order.

Finding a person's name in an unordered guest list.

Looking up a phone number in a sorted phone book.

Checking whether a number is present in a list of sorted lottery numbers.

Linear search is suitable for unsorted lists, such as an unordered guest list, where binary search wouldn't be efficient.

Submit