Images

Objectives

• Understand what a pixel is and be able to describe how pixels relate to an image and the way images are displayed.
• Describe how a bitmap represents an image using pixels and colour depth
• Explain the following for bitmaps:
  • image
  • colour depth
• Describe using examples how the number of pixels and colour depth can affect the file size of a bitmap image
• Calculate storage requirements for bitmapped images and be aware that bitmap image files may also contain metadata.
• Be able to convert binary data into a bitmap image
• Be able to convert binary data into a bitmap image

The storing and processing of images is another important feature of computer systems. The data for the image has to be stored as binary patterns and there are two main methods:

• bit-mapped graphics: data is stored as a grid of elements, each element representing a colour being used
• vector graphics: individual shapes are stored as a set of instructions used to recreate the graphic

For GCSE we only need to know how bitmap is used to represent images.

Bit-mapped graphics

The bitmap, as the name suggests, is a map of bits implying an underlying array structure with rows and columns. At each intersection is a picture element, or pixel which is the smallest identifiable element of an image. The pixel is the building block that builds any image, font, screen that you see. Each pixel will have a single numeric value, this value represents the colour of the pixel.

If an image is opened with any image editing program on the computer and we zoom in on that image the pixels become visible as individual squares, as shown in the following image:

This occurs because the image is being displayed with a lower dots per inch density and is known as pixellation.

Note

Many of the common file formats we use for storing and representing images will use this format including .BMP, .JPG, .PNG though many will also apply sophisticated compression techniques which we'll consider later.

There are two aspects of any bit-mapped image which impact the quality of that image (ignoring any compression for now):

• Resolution (or image size)
• Bit depth (or Colour Depth)

Image Resolution

There are two ways to define the resolution of an image:

1. The number of pixels that an image contains per inch, expressed as either pixels per inch (PPI) or dots per inch (DPI). This of also called the pixel density. It specifically refers to the number of pixels per inch in a printed image. The higher the pixel density (a higher PPI or DPI) the sharper the image.
2. The total number of pixels in an image. This definition is related to the size of the image file itself. It is calculated by multiplying the number of pixels in the width of the image by those in the height of the image. The greater the number of pixels the better the quality of the image.

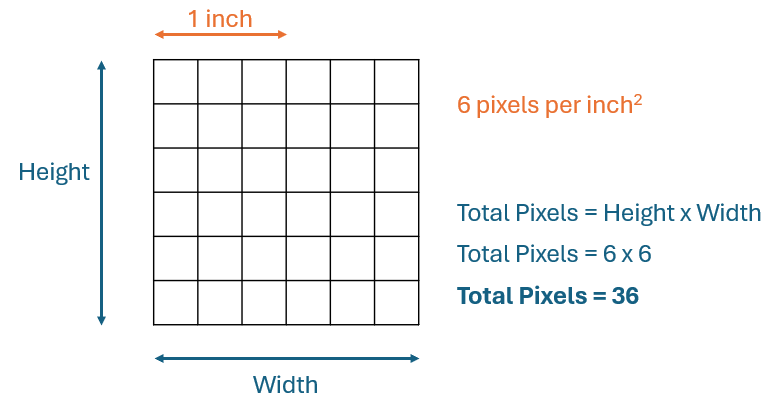
Both of these values will impact on how clear of sharp the image will be as well as determining the size of the image when printed.

So, by example, an image with pixel resolution of \(6000 \times 4000\) means the image is \(6000\) pixels wide and \(4000\) pixels high. In total, the image contains \(24,000,000\) pixels or \(24 \text{MP}\). This is a fairly typical resolution used by cameras today (2022)

The final printed size of an image depends on the DPI. If an image has a resolution of \(4500 \times 3000\) pixels the image will print at \(15 \times 10\) inches at 300 DPI. If the DPI was changed to 72 it will use \(62.5 \times 41.6\) inches due to the lower DPI.

Most operating systems can display the resolution of an image, as in the example below (Windows), here by right-clicking on the image and selecting the option 'Properties' from the menu. This is a small image \(311 \times 162\) pixels or \(50,382\) pixels.

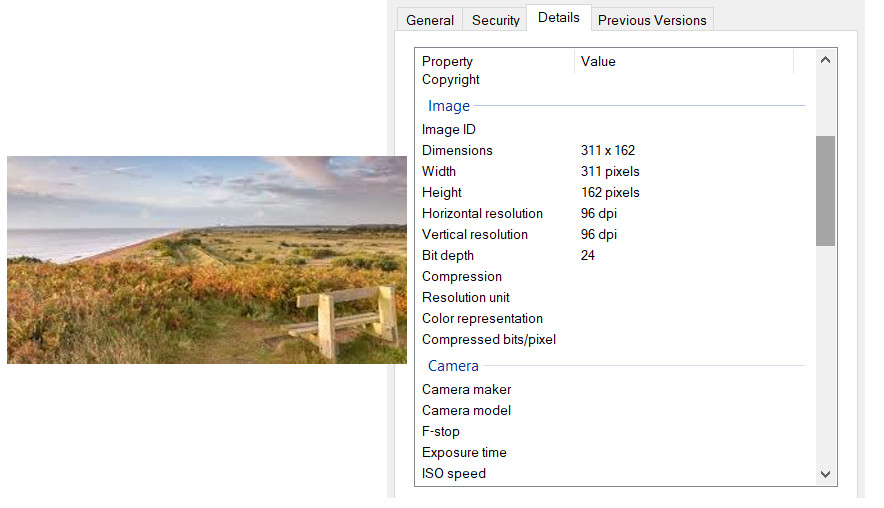
In the properties window above is also shown the pixel density, the dots per inch.¹

Simplistically one might think of the pixel resolution of the image as an input measurement, and DPI as an output measurement. So, 300 dpi means e.g. the printer will output 300 tiny dots for every inch of the print. Any image can be displayed at any dot density.

Note

The print size has changed but the image itself has not been resized, it's merely reorganised the pixels. The same thing happens when you change the resolution of your monitor, a higher resolution is making each pixel smaller and the smaller the icons, text etc will appear.

Colour Depth

Each pixel represents a colour, each colour will be represented internally by a binary value. The number of bits being allocated to each pixel will determine the colour depth, also known as the bit depth as it tells us how many bits have been used for that colour.

For a monochrome (2-colour) image we only need 1 bit per pixel with \(1\) for black and \(0\) for white:

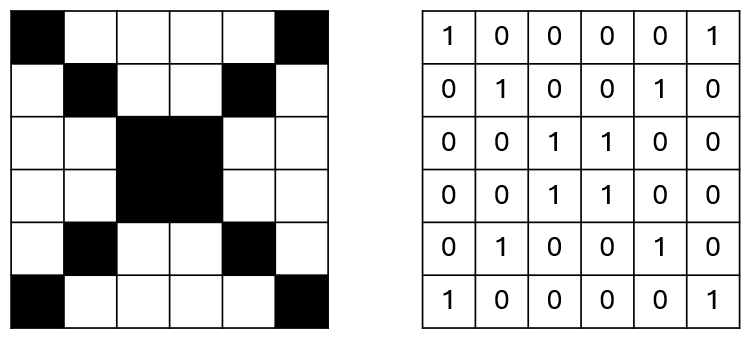
If we want more colours then we have to increase the number of bits being used to store the value representing the colour. By using 2 bits we know have 4 possible colours:

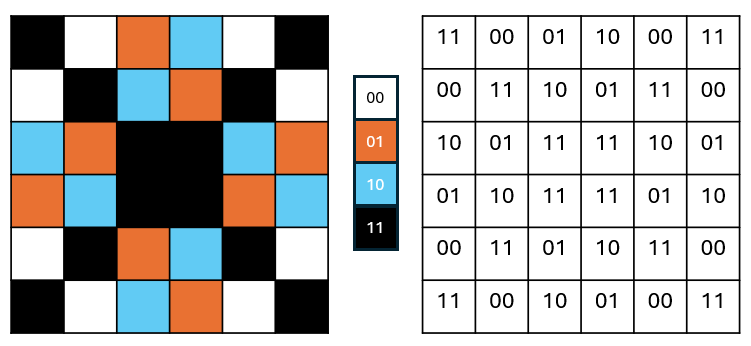
Note

Remember: \(2^2 = 4\)

Thus, \(8\) bits will provide \(256\) possible colours.

As for all types of binary data, the general formula is that for \(n\) bits you can store \(2^n\) colour codes, so more bits being allocated to each pixel will yield more colours being available and the more photo-realistic will be the final image:

Modern displays will use a combination of red, green and blue to form the colours. Each of these colours can be allocated 8-bits giving 24-bits in total. This amounts to \(2^{24}\) colours (16.7 million possible colours). It is believed the human eye can only distinguish about 10 million colours so this is sufficient and is often known as true colour.

You will also encounter 32-bit colour depth, an extra byte being added. This extra 8 bits is usually used as an alpha or transparency byte, frequently termed as the alpha channel, which adjusts the level of opacity for a pixel when being blended with other colours. This makes the pixel translucent, or "see-through".

Do not get confused between the number of colours and the colour depth. Colour depth is the number of bits allocated to the values representing the colours.

Increasing the colour depth will inevitably lead to a larger file size.

Print quality vs web page quality

Images that are created to be displayed on a web page are typically \(72 dpi\). When printing the image the resolution needs to be higher, and is typically \(300 dpi\).

Calculating file size for an image

There are two measurements to consider:

• resolution of the image, i.e. the number of pixels being used
• the colour depth for each pixel

It's a relatively simple calculation:

\(filesize = (\text{ number of pixels } \times \text{ bits per pixel })\)

Thus, is \(12\) bits are used per pixel in an image \(800\) bits wide and \(600\) bits tall:

• Number of pixels = \(800 \times 600\)
• Colour depth = \(12\)
• Total number of bits = \(800 \times 600 \times 12\) = \(5760000\)
• Total number of bytes = \(5760000 / 8\) = \(720000\) bytes

Note

Many images will use compression to reduce the size of the file

Image metadata

The actual size of the file saved to a disk will be higher than that calculated above. The reason being that along with the data about each individual pixel will be data about the image itself, known as the metadata, and usually stored in the header of a file. The metadata includes image about the the image itself as well as information about how it was produced. Typically this might include e.g.:

• the format of the file
• the dimensions, in pixels
• data information i.e. when created, when last modified etc
• the device used to take the image, and if camera any specific details about aperture size etc
• geographical location
• colour depth used

The properties image above showed the metadata available for that image.

Image processing with Python

To extend some of this theory we can see how to work with images using Python.

Exercise 1: Load and Display an Image

Use a Python library like PIL (Pillow) to load and display an image. You can install Pillow using pip install Pillow. Here's a sample code:

from PIL import Image
import matplotlib.pyplot as plt

# Load an image
image_path = "dunwich.jpg"
img = Image.open(image_path)

# Display the image
plt.imshow(img)
plt.axis('off')
plt.show()

Output from this code:

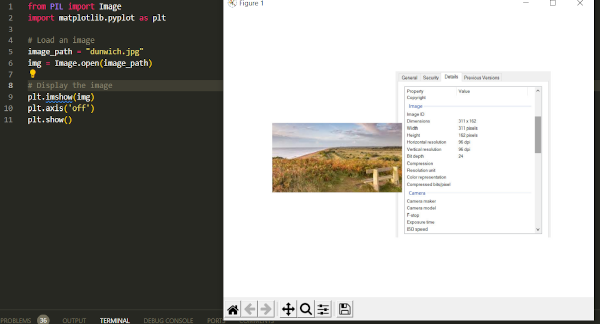
Exercise 2: Retrieve image resolution

Using the same PIL (Pillow) package we can return the dimensions and resolution of a given image:

from PIL import Image
import matplotlib.pyplot as plt

with Image.open("dunwich.jpg") as image:
    width, height = image.size
    xres, yres = image.info['dpi']

print(f"Width: {width}")
print(f"Height: {height}")
print(f"Resolution: {xres} x {yres}")

Exercise 3: Convert Image to Grayscale

Explore how colors are represented in images by converting the image to grayscale. Grayscale images represent each pixel with a single intensity value (typically from 0 to 255).

image_path = "dunwich.jpg"
img = Image.open(image_path)
# Convert image to grayscale
gray_img = img.convert('L')

# Display the grayscale image
plt.imshow(gray_img, cmap='gray')
plt.axis('off')
plt.show()

Output from this code:

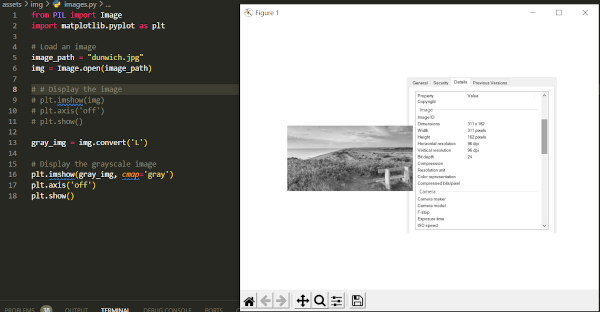
Exercise 4: Resize Image

Understand the impact of image resolution by resizing the image. You can use the resize() method from Pillow.

# Resize the image
new_size = (300, 200)
resized_img = img.resize(new_size)

# Display the resized image
plt.imshow(resized_img)
plt.axis('off')
plt.show()

Exercise 5: Flip Image Horizontally or Vertically

Explore how images can be manipulated by flipping them horizontally or vertically.

# Flip the image horizontally
flipped_horizontal_img = img.transpose(Image.FLIP_LEFT_RIGHT)

# Flip the image vertically
flipped_vertical_img = img.transpose(Image.FLIP_TOP_BOTTOM)

# Display the flipped images
plt.subplot(1, 2, 1)
plt.imshow(flipped_horizontal_img)
plt.axis('off')
plt.title('Horizontal Flip')

plt.subplot(1, 2, 2)
plt.imshow(flipped_vertical_img)
plt.axis('off')
plt.title('Vertical Flip')

plt.show()

Output from the previous code:

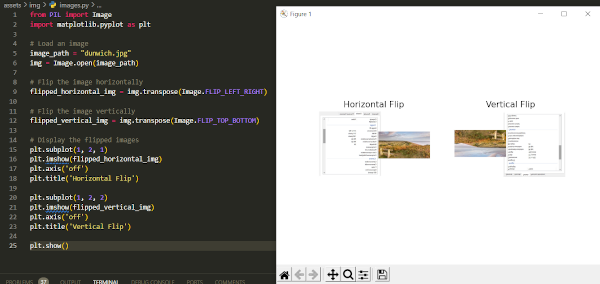
Exercise 6: Extract Image Channels (RGB)

Explore how color images are represented using the RGB model. Extract and display individual color channels (Red, Green, Blue).

# Split the image into RGB channels
r, g, b = img.split()

# Display individual color channels
plt.subplot(1, 3, 1)
plt.imshow(r, cmap='Reds')
plt.axis('off')
plt.title('Red Channel')

plt.subplot(1, 3, 2)
plt.imshow(g, cmap='Greens')
plt.axis('off')
plt.title('Green Channel')

plt.subplot(1, 3, 3)
plt.imshow(b, cmap='Blues')
plt.axis('off')
plt.title('Blue Channel')

plt.show()

Output from previous code:

Questions

1. What is a pixel, and how does it relate to the display of images?

A pixel is a unit of sound that creates audio output.

A pixel is a small unit of an image that, when combined with others, forms a complete picture.

A pixel is a type of file format used to store images.

A pixel is a mathematical formula used to create colors in digital images.

A pixel is the smallest unit of a digital image, and when many pixels are combined, they form a complete image.

Submit

2. How does a bitmap represent an image using pixels and color depth?

By storing only the outline of the image.

By assigning a specific color to each pixel based on its color depth.

By converting the image into a text format.

By using mathematical equations to represent the image.

A bitmap represents an image by assigning a specific color to each pixel based on the image's color depth, which defines how many colors can be displayed.

Submit

3. What is meant by 'color depth' in the context of bitmap images?

The number of colors that can be displayed by a pixel.

The physical depth of the screen displaying the image.

The amount of storage required to save an image.

The resolution of the image.

Color depth refers to the number of bits used to represent the color of a single pixel, affecting the range of colors that can be displayed.

Submit

4. How does the number of pixels in an image affect its file size?

The more pixels, the larger the file size, and the higher the level of detail.

The fewer pixels, the larger the file size.

File size is not related to the number of pixels.

The number of pixels only affects the image quality, not the file size.

An image with more pixels will have a larger file size and a higher level of detail, as each pixel requires storage space.

Submit

5. If an image has a resolution of 800x600 pixels and a color depth of 24 bits, how many bits are used to represent the image?

480,000 bits

14,400,000 bits

11,520,000 bits

4,800,000 bits

The total number of bits is calculated by multiplying the resolution (800x600 pixels = 480,000 pixels) by the color depth (24 bits per pixel), resulting in 11,520,000 bits.

Submit

6. What is the significance of 'storage requirement' in relation to bitmapped images?

It refers to the amount of space needed to store the image file.

It defines the color of each pixel in the image.

It describes the method used to compress the image.

It determines the physical size of the display screen.

The storage requirement is the amount of space needed to store a bitmap image file, which depends on the image's resolution and color depth.

Submit

7. Why is it important to be aware that bitmap image files may contain metadata?

Metadata can reveal the image's color depth.

Metadata may include information such as the image's creation date, author, or location, which can be sensitive.

Metadata determines the image's file format.

Metadata can reduce the file size of the image.

Metadata may contain additional information about the image, such as the creation date or location, which could be sensitive and should be handled carefully.

Submit

8. Which of the following best explains how the color depth of a bitmap image influences its file size?

Higher color depth decreases the file size.

Higher color depth increases the file size, as more bits are needed per pixel.

Color depth has no impact on file size.

Lower color depth always results in better image quality.

Higher color depth increases the file size because more bits are required to represent each pixel's color.

Submit

9. What is the relationship between the resolution of a bitmap image and its level of detail?

Higher resolution means fewer details can be captured.

Lower resolution improves image quality.

Higher resolution means more details can be captured, as there are more pixels per image.

Resolution does not affect the level of detail.

Higher resolution allows for more details to be captured in an image because there are more pixels available to represent the visual information.

Submit

10. What is a simple example of how bitmap images are represented using pixels and color depth?

A 1x1 pixel image with a color depth of 1 bit can be either black or white.

A 10x10 pixel image with a color depth of 8 bits per pixel can only be monochrome.

An image with no pixels cannot display any colors.

Color depth only affects the number of pixels in an image.

In a bitmap image, a simple example would be a 1x1 pixel image with a 1-bit color depth, meaning the image can only be black or white.

Submit

---

1. The density of pixels in a monitor is measured in dots per inch (DPI) but since it refers to the number of dots that are within a line of one inch of scan, they were discontinued in favor of PPI (pixels per inch). While PPI is the correct term to refer to monitors, the two are often used interchangeably. ↩